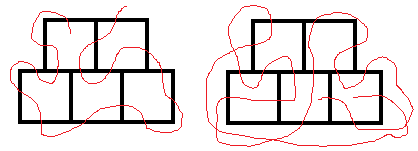
Sorry, but this is provably impossible. The puzzle can be quite easily transformed into the equivalent graph: each square, plus the outer region, is a node. Each line segment is represented by an edge on the graph.
The resulting graph, which is equivalent to the original puzzle, looks like this:

The number of edges leading from each node is 5, 5, 5, 5, 5, and 11. There are six nodes with an odd number of edges; however, it is only possible to find an
Euler path on a graph with two or zero such nodes. Therefore, the puzzle has no solution.
Note also that any
solvable puzzle of this nature may be solved
algorithmically; that is to say, it's hardly a puzzle at all.
EDIT: Also, if you don't have to pass through half-segments as though they are distinct, Amadeus's solution is correct. My post regards the other case, which is apparently the one which you were trying to solve.